By Saeed Mirshekari
February 28, 2014
Access O'Mentors
Top Data Scientist Mentors from Fortune 500 Companies excited to help you out 1-on-1!
1️⃣ Explore freely
→
2️⃣ Apply confidently
→
3️⃣ Pay securely
→
4️⃣ Book instantly
Abstract
Will Living People Ever Outnumber the Dead? Probably not! It has been shown that only about 6.5 percent of all people ever born were alive in 2011 [1]. But the human population on Earth has been growing very rapidly in the recent decades such that one could imagine one day in which the number of alive people reaches the number of all the dead people. Assuming the world's average life expectancy to remain constant and equal to its current value (68 years) and the world's annual growth rate to stay constant but just a bit less than its current value (1%), we show that living people will never outnumber the dead.
Growth of Living Population
The human population has started to grow extremely fast only since the last few centuries, as you can see in Figure 1. The rate of population growth has obviously changed over time. But, because of all the human improvements and developments in the modern world it is not unlikely to reach a constant rate of population growth and life expectancy in the future.
The ''annual population growth rate'' (r) is the rate at which the number of individuals in a population increases in a year as a fraction of the initial population. It is very easy to show that for a constant population rate of r the living population will be growing as [eq.1]
Alive (t) = N_0 (1 + r) x t
where N_0 is the living population at the initial time. Population in the world is currently growing at a rate of about 1.14% per year [2] and the current world's average life expectancy is 67.88 years [3].
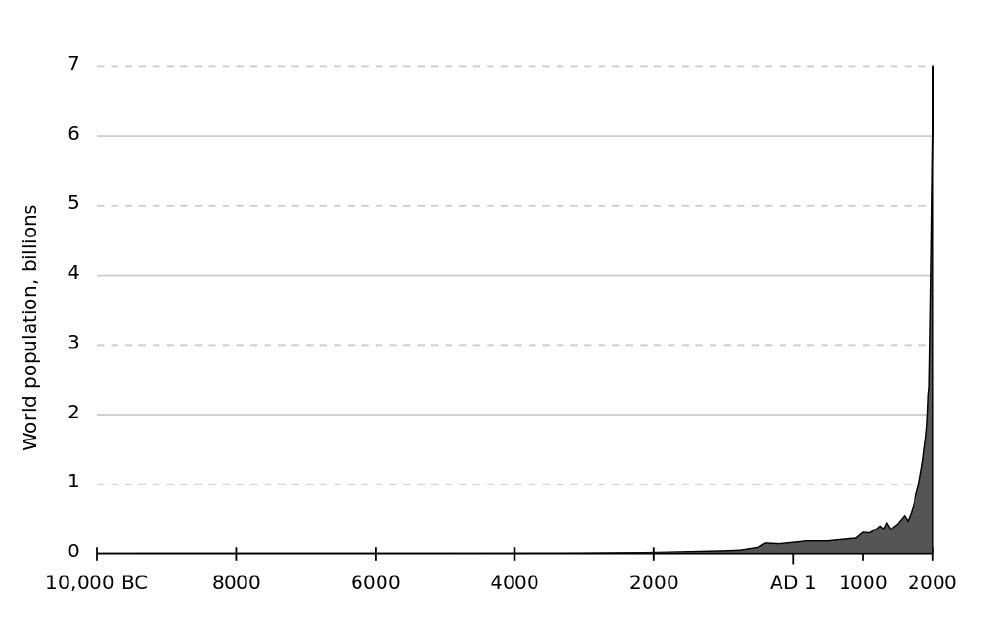Figure 1: The estimated size of human population from 10,000 BCE-2000 CE. [3]
How Many People Are Dead?
Knowing only the constant values of current annual population growth rate, r, and the world average life expectancy, <L>, there is a simple way to estimate the number of dead people at a specific time t>.
Suppose after t0 the annual growth rate and the average life expectancy reach their constant values. The number of living people at this time is given by Equation (1) as Alive(t0). Now the question is that after a single period of the average life expectancy, i.e. at t = t0 + <L> have died in average in this time period? The answer is simply Alive t0. In other words, in average, the number of people who have died since t = t0 until t = t0 + <L> is same as the number of people who were alive at t = t0. Without losing any generality we can set t0 = 0 and generalize this idea to the future times in which t* = N x <L> and write [eq.2]
Dead(t*) = SUM (Alive n([L])) {from n=1 to n=N-1} + Dead(t0)
where N is an integer number and Dead(t0) is the
number of all people who have died at any time in
the history before t = t0. Using Equation (1), the
above summation can get as simplified as [eq.3]
Dead(t) = N0 * [(1 + r) ^ t - 1] / [(1 + r) ^ [L] - 1] + Dead(t0)
Critical Values of r and <L>
Based on Equations (1), (3), it's not difficult to show
the living population ultimately outnumber the dead
if and only if:
(1 + r) x [L] > 2
For example, with the current value of the world average life expectancy, i.e. 67.88 years, the living population can outnumber the dead if and only if the annual population growth rate is not less than the critical value of 1.02%. This number is only slightly smaller than the current value for the world i.e. 1.14%. Although we have considered r to be
constant, recent studies [2] predict a small decrease in the rate of population growth to a value less than 1% in close future. This small decrease would be enough to conclude that the living population never outnumber the dead with the current world average
value of life expectancy.
On the other hand, as another example, if we fix the population growth rate at its current value, the world average life expectancy has to be greater than 61.12 years to ultimately allow the living population outnumber the dead. Any values of r and <L> less than their critical values cause the dead population outnumber the living forever.
References
[1] Carl Haub, http://www.prb.org (2011)
[2] http://www.worldometers.info
- Thanks to M. Le Delliou for useful discussions.
- This calculations might be vey well known and we probably
just have rediscovered them here.
Saeed Mirshekari
Saeed is currently a Director of Data Science in Mastercard and the Founder / Director of OFallon Labs LLC. He is a former research scholar at LIGO team (Physics Nobel Prize of 2017).